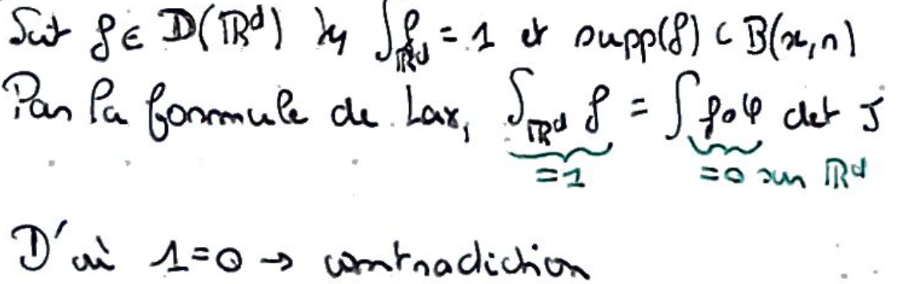Démonstration du théorème de non-rétractation :

On procède par l'absurde et on prend \(x\) dans la différence.
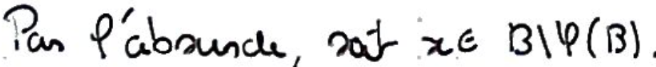
Par continuité, \(\varphi\) est également l'identité sur la frontière de la boule, donc \(x\) est à l'intérieur de celle-ci.
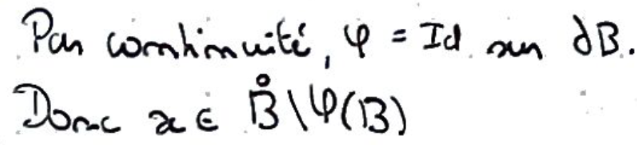
Par ouverture de cette ensemble, on peut en fait prendre une boule autour de \(x\).

C'est absurde d'après le Théorème de Lax, en prenant \(f\in\mathcal C_c({\Bbb R}^d,{\Bbb R}^d)\) quelconque.